Les ordinateurs sont de fabuleuses et infatigables machines de calculs. Mais les résultats qu’ils donnent sont-ils fiables ?
Tester la précision de calcul de son ordinateur :
La précision de calcul est, depuis l’origine de la micro-informatique, une question cruciale.
Dans les années 80, Hebdogiciel, l’hebdomadaire des programmes informatiques, testait la précision de calcul des machines dont il parlait dans ses colonnes à l’aide d’un programme simple mais bougrement efficace.
Voici le code-source du programme (Basic standard) publié dans les colonnes d’Hebdogiciel :
Le programme d’Hebdogiciel calculait la racine carré du chiffre deux (ligne 30 du programme) puis la racine carré du résultat et ainsi de suite, à vingt reprises au total (à l’aide d’une boucle FOR… TO… NEXT). Puis ce dernier résultat est porté à la puissance (ligne 60) de nouveau vingt fois, de sorte que l’on obtienne le chiffre de départ, soit deux… enfin en théorie.
Effectivement, le résultat retourné par le programme (ligne 80) devrait être de 2. Mais qu’en est-il réellement ?
Résultats fournis par des machines des années 80 publiés dans le numéro 61 d’HEBDOGICIEL daté du 14 décembre 1984 (reproduction de l’article complet téléchargeable plus bas) :
– TEXAS TI-99 : 1.999999924
– EXELVISION : 1.999999924
– CANON X07 : 1.9999997741097
– CANON V20 MSX : 1.99999977
– YASHICA MSX : 1.99999977
– AMSTRAD : 1.999433
– ATARI 800 XL : 1.99755243
– ZX 81 : 2.000445
– SPECTRUM : 2.000445
– APPLE IIe : 2.00232917
– APPLE IIc : 2.0023291
– COMMODORE 64 : 2. 00232917
– ORIC ATMOS : 2.00232917
– VIC 20 : 2.00232917
– THOMSON MO5, TO7, TO7-70 : 2.16828
– TANDY TRS-80 : 2.16828
– HECTOR HRX : 2.16927
Certains écarts laissent perplexes…
Origine de l’imprécision du résultat :
A quoi sont dues ces imprécisions ? Simplement, au nombre limité de décimales conservées par le système. L’imprécision des calculs s’accroît au fil des la succession des calculs. Pour information, le format Double (nombres réels en double précision) ne conserve que les quinze premières décimales, ce qui en soit est déjà beaucoup mais pas suffisant dans tous les cas.
Pas d’inquiétude exagérée non plus… La comptabilité ne nécessite pas le même degré de précision que les calculs en astronomie ou en mathématiques. En général, cinq ou six décimales garantissent un degré de précision suffisant pour les calculs comptables courants comme la TVA ou le contrôle de gestion.
Qu’en est-il sur les machines actuelles ?
Les constructeurs nous vantent la rapidité du microprocesseur, l’ergonomie de l’interface du système… mais qu’en est-il de la précision de calcul ?
Je vous propose de tester par vous-même la précision de votre machine à l’aide du même programme que celui utilisé par les journalistes d’Hebdogiciel.
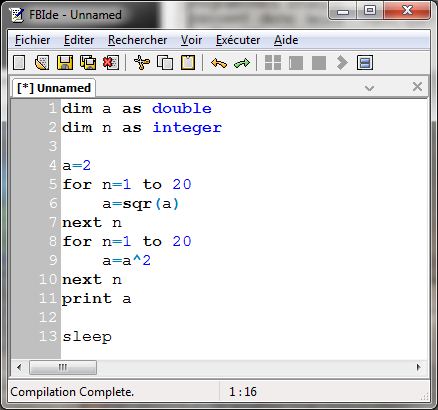
Voici le code-source du programme adapté au freeBasic (cf http://www.auditsi.eu/?p=1623 pour s’initier à ce langage) :
dim a as double dim n as integer a=2 for n=1 to 20 a=sqr(a) next n for n=1 to 20 a=a^2 next n print a sleep
Le code-source et le programme exécutable sont disponibles en téléchargement en bas de cet article.
N’hésitez pas à le tester sur votre propre machine et à poster en commentaire votre propre résultat.
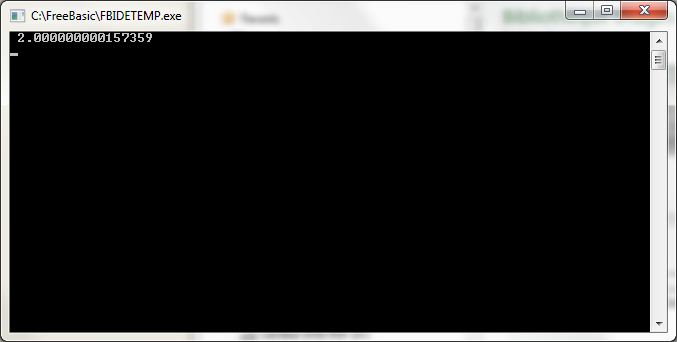
Mon DELL LATITUDE E6520 renvoie 2.000000000157359. Pas mal, mais ce résultat ne correspond pas tout à fait au chiffre de départ, 2.
Approfondir le sujet :
Histoire de l’informatique / L’informatique des années 80 / Ma collection / Ma documentation
HEBDOGICIEL n°61 daté du 14 décembre 1984 - Article précision calcul.pdf
Derniers articles parBenoît RIVIERE (voir tous)
- Dématérialisation de la facturation : nouvelles mentions obligatoires - lundi 28 octobre 2024
- Interpréteur de formules de calcul en Python - dimanche 13 octobre 2024
- Les données de la facturation électronique - mercredi 9 octobre 2024
- VBA/SQL vs Power Query : deux solutions complémentaires - mercredi 2 octobre 2024
- L’IA dans les cabinets comptables : cas concrets - jeudi 26 septembre 2024
toujours intéressant de tester les performances de son ordinateur
j’ai essayé et j’obtiens exactement le meme chiffre que vous
bizarre car le mien est un lenovo
peut-etre une limite liée au processeur ?
Bonjour,
Le fait que l’on obtienne des résultats identiques sur des machines différentes (processeurs différents mais il est vrai de même famille) semble indiquer que c’est la gestion de la précision des calculs par freeBasic qui est en cause. A confirmer par d’autres résultats…